Elliptical Orbit
In astronomy, a satellite is something that orbits around a more massive object, called a primary.
The Moon orbits the Earth, so the Moon is the satellite and the Earth is the primary. Earth orbits the Sun, so the Earth is the satellite and the Sun is the primary. As you can see, a satellite of one system (Earth-Sun) can be the primary of another system (Earth-Moon).
Satellites actually orbit in ellipses, which are ovals. There is a value called eccentricity (e) which determines the shape of an ellipse. Circles are a special type of ellipse, where the eccentricity e = 0.
A satellite orbiting at a distance r from the massive object needs to travel at a very specific speed to travel in a circle. At all other velocities it will travel in ellipse.
You can see an elliptical orbit here:
https://www.glowscript.org/#/user/zorniy/folder/Public/program/planete
Properties of ellipses
Before we start with elliptical orbits, we need to learn some properties of ellipses.
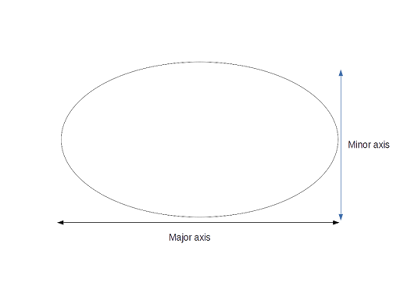
Major and Minor Axis
The length of the longer side is the major axis, while the length of the shorter side is the minor axis.
Eccentricity
Next is the eccentricity e.
$e = \sqrt{1-\frac{b^2}{a^2}}$
Eccentricity determines the "ovalness" of the ellipse.
- $e=0$ is a circle. In the equation above, if b = a then e = 0 and the major axis is the same length as the minor axis.
- e between 0 and 1, $0 < e < 1$ is an ellipse
- $e = 1$ is a parabola. It is not a closed shape. An object travelling in a parabolic path will go out into space and not return.
- $e > 1$ is a hyperbola. It is not a closed shape. An object travelling in a parabolic path will go out into space even faster and not return.
Periapsis and Apoapsis, Eccentric Anomaly $\theta$ and Orbital Distance r