Bab 2

Pergerakan pada Halaju Konstan

Dalam bab ini kita akan mengkaji pergerakan pada halaju konstan.

Kita bayangkan suatu objek yang bergerak pada halaju yang sama, dan tidak bertukar arah.  Maka sesaran yang dialami oleh objek itu diberi formula:

$s = ut$

Di mana:

    s adalah sesaran
    u adalah halaju
    t adalah masa

Sesuatu objek yang bergerak pada halaju u selama masa t akan bergerak sebanyak s.

Applet di bawah menunjukkan graf sesaran s melawan masa t. Gerakkan "slider" untuk mngubah nilai v. 

"Slider" boleh digerakkan dengan menggunakan mouse. Anda juga boleh klik atas slider dan gerakkannya menggunakan kekunci panah (arrow keys) kiri dan kanan. 

Graf boleh digerakkan dengan mouse. Paksi x dan paksi y boleh diubah skala dengan menekan butang "shift", dan sekaligus klik atas paksi dan menyeret (drag). 

Jika menggunakan tablet ataupun telefon pintar, gunakan jari-jari anda ke atas paksi untuk mengubah skala paksi.

 

1.     Gerakkan "slider" supaya v = 1. Berapakah sesaran pada masa t = 4 ?
   
   
2.     Gerakkan "slider" supaya v = 3. Berapakah sesaran pada masa t = 2.5 ?
   
   
3.     Gerakkan "slider" supaya v = 0.5. Berapakah sesaran pada masa t = 6?
   
   
4.     Gerakkan "slider" supaya v = 1.5. Menurut graf, berapakah masa yang diambil untuk bergerak sejauh 3m?
   
   
5.     Gerakkan "slider" supaya v = 2. Menurut graf, berapakah masa yang diambil untuk bergerak sejauh 3m?
   
   
6.     Gerakkan slider agar garisan lurus itu melalui t = 4 dan s = 1. Apakah nilai v yang kamu dapati?
   
   
7.     Gerakkan slider agar garisan lurus itu melalui t = 3 dan s = 4. Apakah nilai v yang kamu dapati?
   
   
8.     Gerakkan slider agar garisan lurus itu melalui t = 4 dan s = 4. 

• Apakah nilai v yang kamu dapati? Cuba kira kecerunan graf tersebut. 
• Apakah hubungan v dengan kecerunan garis dalam graf s vs t?




Kinematik 1

 Alkisah tersebutlah kisah...

Dalam Bab ini kita akan mengkaji pergerakan suatu objek dalam beberapa keadaan:

• Objek yang bergerak pada halaju konstan atau malar
• Objek yang bergerak dengan pecutan konstan

Pergerakan Halaju Konstan

Kita membayangkan sesuatu objek bergerak dan halajunya tidak berubah. Pecutan a adalah sifar. 

 Applet di bawah menunjukkan graf sesaran vs masa, yang menunjukkan perubahan sesaran menurut masa pada halaju tetap.

$$s = vt$$

Di mana

•  s adalah sesaran
• v adalah halaju
• t adalah masa
  

 Gerakkan slider pada graf tersebut untuk mengubah nilai halaju v

 

 

1. Apakah kesan terhadap kecerunan graf jika nilai v diubah?
2. Bagaimanakah nilai perubahan nilai sesaran menurut masa, jika halaju adalah negatif?
   

Gravity (Part 3)

 Elliptical Orbit

In astronomy, a satellite is something that orbits around a more massive object, called a primary. 

The Moon orbits the Earth, so the Moon is the satellite and the Earth is the primary. Earth orbits the Sun, so the Earth is the satellite and the Sun is the primary. As you can see, a satellite of one system (Earth-Sun) can be the primary of another system (Earth-Moon).

Satellites actually orbit in ellipses, which are ovals. There is a value called eccentricity (e) which determines the shape of an ellipse. Circles are a special type of ellipse, where the eccentricity e = 0.

A satellite orbiting at a distance r from the massive object needs to travel at a very specific speed to travel in a circle. At all other velocities it will travel in ellipse.

You can see an elliptical orbit here:

https://www.glowscript.org/#/user/zorniy/folder/Public/program/planete

 

Properties of ellipses

Before we start with elliptical orbits, we need to learn some properties of ellipses. 

 

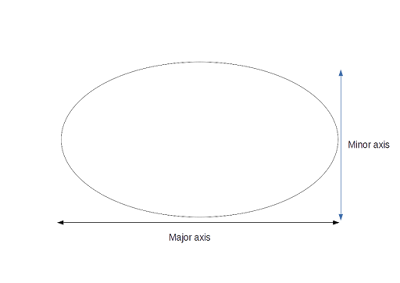
Major and Minor Axis

The length of the longer side is the major axis, while the length of the shorter side is the minor axis.

 

We are more interested in the semimajor axis, a and semiminor axis, b,which are simply the major and minor axis divided by 2.

 

semimajor axis $a = \frac{major}{2}$

semiminor axis $b = \frac{minor}{2}$

 

 

Eccentricity

Next is the eccentricity e. 

$e = \sqrt{1-\frac{b^2}{a^2}}$

Eccentricity determines the "ovalness" of the ellipse.  

• $e=0$ is a circle. In the equation above, if b = a then  e = 0 and the major axis is the same length as the minor axis.
  
• e between 0 and 1, $0 < e < 1$ is an ellipse
• $e = 1$ is a parabola. It is not a closed shape. An object travelling in a parabolic path will go out into space and not return.
• $e > 1$ is a hyperbola. It is not a closed shape. An object travelling in a parabolic path will go out into space even faster and not return. 

 

Periapsis and Apoapsis, Eccentric Anomaly $\theta$ and Orbital Distance r

 

 

 

 

Gravity(Part 2)

Simple Circular Orbit

Consider an object with mass m orbiting a planet with mass M, at a distance r from the planet, in a circular orbit, with velocity v.  

 

 

 

You  may see a VPython animation of a circular orbit here:

https://www.glowscript.org/#/user/zorniy/folder/Public/program/CircularOrbit 

 

Or a little video of the program running:

 

 

 

There are two forces acting on the object:

• Gravity, pulling inwards towards the planet
• Centrifugal force, acting outward

In a circular orbit, the distance r remains the same, meaning there is no acceleration outwards or inwards.

According to Newton's Second Law:

$F_{total} = ma$

gravity + centrifugal = 0

$-\frac{GMm}{r^2} + \frac{mv^2}{r} =0$

$\frac{mv^2}{r} = \frac{GMm}{r^2}$

$v^2 = \frac{GM}{r}$

We obtain the velocity of the object orbiting in a circular orbit:  

$v = \sqrt{\frac{GM}{r}}$

This velocity must be tangential to the orbit, or at right angles to the vector r between the object and the planet.

Orbital Period

The orbital period T is the time taken to complete one full orbit. In physics, the result of the calculation will be in seconds.

 

If we multiply the orbital velocity v with the orbital period T, we get the total distance traveled, which is equal to the circumference of a circle.

$vT = 2\pi r$

 

$T = \frac{2 \pi r }{v}$

 

But  $v = \sqrt{\frac{GM}{r}}$

 

$T = 2 \pi r \sqrt{\frac{r}{GM}} $ 

So we arrive at the orbital period:

$T = \frac{2 \pi}{\sqrt{GM}} r^{3/2}$

We can calculate the orbital period T if we know the mass of the central mass M and the distance r.

 

But we can also use it to calculate the mass of a planet, if we can measure the orbital period of its satellite and the orbital distance. 

This is how the masses of planets and other stars were calculated; astronomers observed something that orbited them. Astronomers measured the time for the satellite to complete one orbit, and measured the separation between the satellite and the planet.

$T^2 = \frac{4 \pi^2}{ GM }r^3 $

$M = \frac{4\pi^2}{GT^2}r^3$

 

There is a moon called Ganymede orbiting the planet Jupiter. Its orbital period is 172 hours, and it orbits 1,070,400 km from Jupiter.

$T = 172 \times 60 \times 60 s = 6.19 \times 10^{5} s$

$r = 1.07 \times 10^9 m$

$G = 6.67 \times 10^{-11}$

Mass of planet Jupiter:

$M = \frac{4\pi^2}{6.67 \times 10^{-11} \times (6.19\times 10^5)^2}\times (1.07\times 10^9)^3 = 1.89\times10^{27}kg$

 

 

This is in good agreement with the value in Wikipedia: $1.898 \times 10^{27} kg$

Do the following:

 

 

Google distance of the Moon from Earth, orbital period T of the Moon around Earth. 

• Convert to meters and seconds.
  
• Calculate the mass of Earth using the equation above. 
• Compare with the mass of Earth according to Google. 

Google distance of Earth to the Sun, and the orbital period.

• Convert to meters and seconds.
  
• Calculate the mass of the Sun using the equation above. 
• Compare with the mass of Sun according to Google.

 

Gravity (Part 1)

Newton's Law of Gravitation is given by:

$F = -G \frac{Mm}{r^2}$

Where M and m are the masses of the two objects, r is the distance between them, and G  is the gravitational constant.

You can express it as a vector (in fact if you are simulating motion in a gravitational field you need to express it as a vector):

$\textbf{F}= -G \frac{Mm}{r^2}\hat{\textbf{r}}$

 

where $\hat{\textbf{r}}$ is the unit vector in the direction from the mass M to m.

Gravitational Potential Energy

Gravitational potential energy is defined as the work done to bring an object from a distance r to infinity.

$U =  \int^\infty_r F dr $

$U = \int^\infty_r \frac{-GMm}{r^2} dr$

$U = -GMm \int^\infty_r r^{-2} dr$

$U = -GMm [-r^{-1}]^\infty_r$

$U = GMm \left[\frac{1}{r}\right]^\infty_r$

$U = GMm [0 - 1/r]$

$U = -\frac{GMm}{r}$ 

Conservation of Energy

An object of mass m moving with velocity $v_1$ at distance $r_1$ from a massive body of mass M has the combined gravitational potential energy U and kinetic energy K:

 

$U + K =-G\frac{Mm}{r_1} + \frac{1}{2}mv_1^2$

If no energy is added into the system by using an engine, this total is conserved. At distance $r_2$ and velocity $v_2$ we will find the total is the same.

$-G\frac{Mm}{r_1} + \frac{1}{2}mv_1^2 = -G\frac{Mm}{r_2} + \frac{1}{2}mv_2^2$

If we know the speed of an object at one distance, we can predict the velocity when the object is at a different distance.

Escape Velocity

Imagine you are standing on the surface of the Earth, and tossed a ball up. You will see the ball gradually slow down, briefly stopping in the air, and then come down again. If you throw the ball hard enough, the ball will slow down, and it will stop at infinity! This means the ball has completely escaped. The velocity that you throw the ball so that it escapes is called the escape velocity.

When you are standing on the Earth, the surface is about 6371 km from the centre.

$r_1 = 6.37 \times 10^6 m$

When the ball reaches infinity, the velocity is zero:

$r_2 =\infty$

$v_2 = 0$

We want to find the escape velocity, $v_1$.

Using the principle of conservation of energy:

$-\frac{GMm}{r_1} + \frac{1}{2} mv_1^2 = \frac{GMm}{\infty} + \frac{1}{2}m (0)^2 $

$ \frac{1}{2} mv_1^2 = \frac{GMm}{r_1}$

$ \frac{1}{2} v_1^2 = \frac{GM}{r_1}$

$ v_1^2 = 2\frac{GM}{r_1}$

$ v_1 = \sqrt{2\frac{GM}{r_1}}$

Putting in the numbers, with $G = 6.67 \times 10^{-11} m^3 kg^{-1} s^{-2}$ and mass of Earth $M=5.97\times10^{24}$:

$v_1 = \sqrt{\frac{2 \times 6.67\times 10^{-11}  \times 5.97\times 10^{24} }{ 6.37\times 10^6}} = 1.09\times 10^4 ms^{-1}$

That is 39,240 km/h.

What if you are already in space, at some distance away from the Earth? Let's say at a distance where $r_1 = 20000 km$? I invite you to try calculating it.

You can also try to calculate the escape velocity from the surface of other planets such as:

Planet	mass	radius
Mars	$6.39 \times 10^{24} kg$	3389.5 km
Jupiter	$1.898 \times 10^{27} kg$	69911 km
Asteroid Ceres	$9.38 \times 10^{20}$ kg	470 km

MathJax Test

I've been struggling to include Mathjax in Blogger properly to write proper mathematical equations. A lot of people saying "paste this here", but this is the only one that worked:

http://holdenweb.blogspot.com/2011/11/blogging-mathematics.html

So here's a little test:

$x^2$

The Fourier Transform is given as:

$F(k) = \int^{\infty}_{-\infty} f(t) e^{-2 \pi k t} dt$

 ...and I happy.

For Blogger, you need to open the Theme, then Cutomize->Edit HTML 

Then copy and paste the code kindly provided in the link above, which I have copied below. Use Ctrl-F to find < /head >. You need to paste it before the < /head >
<script type="text/x-mathjax-config"> MathJax.Hub.Config({tex2jax: {inlineMath: [['$','$'], ['\\(','\\)']]}}); </script> <script src="http://cdn.mathjax.org/mathjax/latest/MathJax.js?config=TeX-AMS-MML_HTMLorMML" type="text/javascript"> </script>